Bonjour à tous !
J'ai crée (ou trouvé) une fonction sympathique et j'aimerai tracer sa courbe représentative sur l'intervalle [0,50]. Voici l'équation en question :
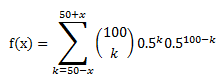
Sauriez-vous comment je peux tracer cette fonction sur Excel ? Sur la calculatrice Casio Graph 35+, on ne peut insérer de somme dans les fonctions malheureusement, et je n'ai que cette calculatrice ...
Pour ceux qui sont curieux, cette fonction donne la probabilité d'obtenir entre (50+x) et (50-x) fois "pile" ou "face" (c'est la même chose) sur 100 lancers. Ou plutôt, je me demandais quelle était l'allure de la courbe lorsqu'on augmentait l'intervalle centré autour de 50.
Merci beaucoup de votre aide, je sais que la demande est probablement inédite ici, et assez particulière.
A très bientôt je l'espère ! >:^D
J'ai crée (ou trouvé) une fonction sympathique et j'aimerai tracer sa courbe représentative sur l'intervalle [0,50]. Voici l'équation en question :
Sauriez-vous comment je peux tracer cette fonction sur Excel ? Sur la calculatrice Casio Graph 35+, on ne peut insérer de somme dans les fonctions malheureusement, et je n'ai que cette calculatrice ...
Pour ceux qui sont curieux, cette fonction donne la probabilité d'obtenir entre (50+x) et (50-x) fois "pile" ou "face" (c'est la même chose) sur 100 lancers. Ou plutôt, je me demandais quelle était l'allure de la courbe lorsqu'on augmentait l'intervalle centré autour de 50.
Merci beaucoup de votre aide, je sais que la demande est probablement inédite ici, et assez particulière.
A très bientôt je l'espère ! >:^D
Dernière édition:

