Le coefficient devant l'exponentiel doit ressembler à quelque chose comme ça :Yep t'as raison.
@TheQg100, voici le truc de maths qui me faisait chier, pour revenir au sujet principal.
Donc : j'essaye d'avoir la formule explicite de la suite suivante en fonction de n (et oui, des maths ...), le but final étant de déterminer sa limite en +infini :
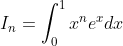
J'avais commencé par une intégration par parties pour trouver une relation de récurrence. On pose :
d'où=x^{n}\\&space;v(x)=e^{x}&space;\end{matrix}\right.)
=\frac{x^{n+1}}{n+1}\\&space;v'(x)=e^{x}&space;\end{matrix}\right.)
On a donc :
v(x)&space;\end{bmatrix}_{0}^{1}-\int_{0}^{1}u(x)v%27(x)dx=\begin{bmatrix}&space;\frac{x^{n+1}e^{x}}{n+1}&space;\end{bmatrix}_{0}^{1}&space;-&space;\int_{0}^{1}\frac{x^{n+1}}{n+1}e^{x}dx&space;=&space;\frac{e}{n+1}-\frac{1}{n+1}I_{n+1})
En multipliant par n+1 de chaque côté et en réarrangeant, on obtient :
I_{n})
Après j'ai déterminé les premiers termes de la suite pour voir ce que ça donnait, genre si on pouvait faire apparaître une formule explicite directement. Et cela donne (en bref) :
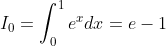
I(1) = 1
I(2) = e - 2
I(3)= 6 - 2e
I(4) = 9e - 24
I(5) = 120 - 44e
I(6) = 265e - 720
I(7) = 5040 - 1854e
etc ...
Là j'ai vu une factorielle apparaître en fonction de n, ainsi qu'un (-1)^n et une autre suite pour le coefficient devant e. En clair :
^{n}&space;[&space;a_{n}e&space;-&space;n!&space;])
Et je ne trouve pas la suite an en fonction de n, help !
(J'ai démontré l'existence de cette limite aussi si tu veux, en montrant que la suite est strictement positive et décroissante ^^ EDIT : cette parenthèse n'est pas pour montrer mes chevilles).
Pour I(0), a0 = 1 = (0 + 1) = (0 - (-1)^(1))
Pour I(1), a1 = 0 = (1 x 1 - 1) = (1 x 1 - (-1)^(2))
Pour I(2), a2 = 1 = (2 x 0 + 1) = (2 x 0 - (-1)^(3))
Pour I(3), a3 = 2 = (3 x 1 - 1) = (3 x 1 - (-1)^(4))
Pour I(4), a4 = 9 = (4 x 2 + 1) = (4 x 2 - (-1)^(5))
Pour I(5), a5 = 44 = (5 x 9 - 1) = (5 x 9 - (-1)^(6))
Pour I(6), a6 = 265 = (6 x 44 + 1) = (6 x 44 - (-1)^(7))
Pour I(7), a7 = 1854 = (7 x 265 - 1) = (7 x 265 - (-1)^(8))
Voilà en gros ce que j'ai trouvé :
an = (n*((n-1)* ... (1*(0 - (-1)^(1)) - (-1)^2) ... - (-1)^(n)) - (-1)^(n + 1))
Tout ceci est bien dégueulasse je l'avoue, hélas je n'ai pas trouvé le moyen de simplifier davantage l'écriture de an. J'ai constaté qu'à chaque fois, an était dépendant du coefficient qui le précédait :
En résumé :
an = n x an-1 - (-1)^(n+1)
J'espère que ça t'aidera :^)
Dernière édition:


